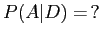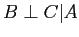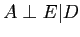Next: Junction Trees
Up: MLA_Exercises_2013
Previous: Factor graphs: HMM
- a)
- [2 P]For the given joint probability draw an appropriate Markov network and
write down the formula for the given conditional probability. Simplify the formula for
the conditional probability as far as possible.
- (i)
-
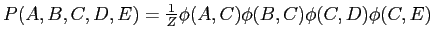 ,
,
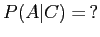
- (ii)
-
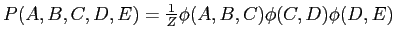 ,
,
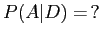
- b)
- [3 P]In this example you have to write down the joint distribution for the given
Markov network and proof that a given independence assumption holds.
- (i)
-
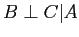
- (ii)
-
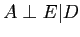
Hubner Florian
2014-01-21
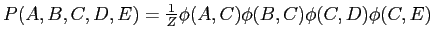 ,
,
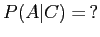
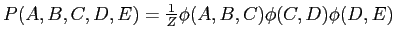 ,
,