


Next: About this document ...
Up: Planning with Approximate Inference
Previous: Task Space Planning with
Try the approach also on a dynamic task.
Now we also want to add the velocities
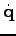 of the joints to our planning scenario. Therefore, we will also incorporate controls
of the joints to our planning scenario. Therefore, we will also incorporate controls
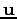 of the robot in our model. The controls
of the robot in our model. The controls
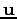 directly represent the accelerations of the joints. The control-dependent state transitions are now given by
directly represent the accelerations of the joints. The control-dependent state transitions are now given by
where
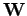 is set to
is set to
![$ \textrm{diag}([10^{-5}, 10^{-5}, 10^{-3}, 10^{-3}])$](img187.png) . Now, in difference to the previous tasks we incorporated controls to our model. For each dimension we will use
. Now, in difference to the previous tasks we incorporated controls to our model. For each dimension we will use 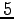 discrete actions
discrete actions
![$ u_{1,2} \in [-4, -2, 0, 2, 4]$](img189.png) , resulting in a action space of
, resulting in a action space of 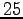 actions. The actions are unknown, and hence, like every unknown hidden variable, they can be integrated out :
actions. The actions are unknown, and hence, like every unknown hidden variable, they can be integrated out :
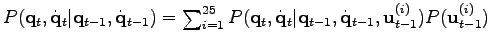 . The term
. The term
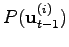 denotes the action prior, similarly to the previous example we again use it to code our laziness, i.e. we prefer doing no action at all
denotes the action prior, similarly to the previous example we again use it to code our laziness, i.e. we prefer doing no action at all
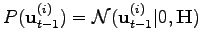 , where
, where
 is set to
is set to
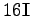 .
.
As we can see the controls are excluded from the inference process, however, they can be easily calculated from an estimated trajectory
![$ [\mathbf{q}_{1:T}, \dot{\mathbf{q}}_{1:T}]$](img196.png) . We will again use a discretization of the state space with a
. We will again use a discretization of the state space with a
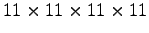 uniform grid. Valid velocities are in the range of
uniform grid. Valid velocities are in the range of ![$ [-1;1]$](img198.png)
- Create the state transition probabilities
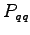 for the dynamic case. Also create the task space mapping
for the dynamic case. Also create the task space mapping 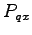 and the collision mapping (both do not depend on the velocities). Use the same intial state and target end-effector position as before, but set the velocity to zero.
and the collision mapping (both do not depend on the velocities). Use the same intial state and target end-effector position as before, but set the velocity to zero.
- Again use Gibbs sampling to sample from valid trajectories. Now use
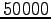 Gibbs sampling steps and
Gibbs sampling steps and 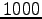 steps between two independent samples. Again calculate the marginals and visualize the marginals of the positions
steps between two independent samples. Again calculate the marginals and visualize the marginals of the positions
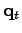 for each time step.
for each time step.
- In addition, plot the expected positions and velocities for each joint over time.



Next: About this document ...
Up: Planning with Approximate Inference
Previous: Task Space Planning with
Haeusler Stefan
2011-01-25
![]() of the joints to our planning scenario. Therefore, we will also incorporate controls
of the joints to our planning scenario. Therefore, we will also incorporate controls
![]() of the robot in our model. The controls
of the robot in our model. The controls
![]() directly represent the accelerations of the joints. The control-dependent state transitions are now given by
directly represent the accelerations of the joints. The control-dependent state transitions are now given by
![]() . We will again use a discretization of the state space with a
. We will again use a discretization of the state space with a
![]() uniform grid. Valid velocities are in the range of
uniform grid. Valid velocities are in the range of ![]()