|
Implement the sum-product algorithm for factor graphs in MATLAB to infer the hidden states of a HMM for the following problem.
An agent is located randomly in a
![]() grid world. In each of
grid world. In each of ![]() time steps he either stays at his current location with a probability of 25% or moves up, down, left or right, where each of these four actions is chosen with a probability of 18.75%. Each cell in the grid world is painted with a certain color that is chosen randomly from a set of
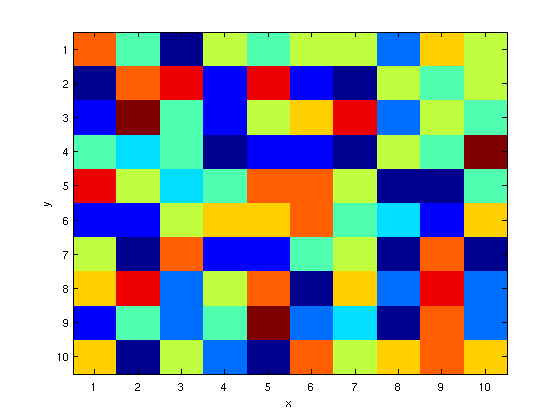
time steps he either stays at his current location with a probability of 25% or moves up, down, left or right, where each of these four actions is chosen with a probability of 18.75%. Each cell in the grid world is painted with a certain color that is chosen randomly from a set of ![]() possible colors as shown in Fig. 3. This color is observed by the agent at each time step and reported to us. Only these color values are available to infer the initial location and the subsequent positions of the agent resulting in the Hidden Markov model (HMM) illustrated in Fig. 4.
possible colors as shown in Fig. 3. This color is observed by the agent at each time step and reported to us. Only these color values are available to infer the initial location and the subsequent positions of the agent resulting in the Hidden Markov model (HMM) illustrated in Fig. 4.
Modify the file hmmMessagePassingTask.m available for download on the course homepage1 and implement the sum-product algorithm to solve this inference problem.
Investigate and discuss the dependence of the solution on the number of different colors in the grid world (![]() ). Hand in figures of representative results that show the actual agent trajectories, the most likely trajectories and the probabilities of the agent positions at each time step as infered by the sum-product algorithm.
). Hand in figures of representative results that show the actual agent trajectories, the most likely trajectories and the probabilities of the agent positions at each time step as infered by the sum-product algorithm.
Present your results clearly, structured and legible. Document them in such a way that anybody can reproduce them effortless. Hand in printouts of your MATLAB code.